円周率の近似

 　今回は様々な方法で円周率を近似してみました。

　円周率は「円周と直径の長さの比」で定義される数学定数です。

「産医師異国に向こう(3.141592653...)」の語呂合わせで覚えた方もいるでしょう。ではそれ以降はどうなっているかというと

↓

3.14159265358979323846264338327950288419716939937510582097499...

と無限に続いていきます。円周率は循環しない小数なので、このような数字の列がランダムに無限に続いていきます。(詳しくは超越数とか踏み込めるのですが今回は割愛します)

　そんな円周率ですが、円を用いてそのまま値を求めることはできないため、何らかの式で近似した値を求めることになります。昔の人は手計算で紙に書いたりいろいろと計算していたのですが、現代ではコンピュータという便利な道具があるので精度の高い数値計算が簡単にできるようになりました。近年では3兆桁まで計算ができるようです。

　今回用いた近似方法は以下のものになります。また、比較として22/7と355/113も出力するようにしています。今回計算した方法はほんの一部なので気になる方は自分で調べてみてください。

・Vieteの公式

・Wallisの公式

・Brounckerの公式

・モンテカルロ法

・Ramanujanの公式

・Gauss=Legendreのアルゴリズム

以下に概要と実装方法例の一部を載せておきます。詳しい証明や導出については略しますので気になる方は各自で調べてみてください。ソースコードへのリンクは一番下にあります。

Vieteの公式

16世紀のフランスの数学者フランソワ・ヴィエトにより発見された公式です。以下のように多重根号の積で表されます。

実装は以下のようになります。Infinity_radical_signは無限根号を計算しています。

  	double Viete(int n){
		int i=0;
		double p=1;
		double data=0;
		for(i=1;i<=n;i++){
			p *= 2/Infinity_radical_sign(2,i);
		}
		p= p * 2;
		return p;
	}
  

Wallisの公式

17世紀にイングランドの数学者であるジョン・ウォリスにより導入されたウォリス積分より導かれる公式です。根号はなく計算は簡単ですが、値の収束が遅いため実用的ではないようです。式は以下の形で表されます

	double Wallis(int n){
		double i=(double)n;
		if(i<=0.0){
			return 2.0;
		}else{
			return ((2 * i) / (2 * i - 1) )*((2 * i) / (2 * i + 1)) * Wallis(i - 1.0);
		}
	}
  

Brounckerの公式

イングランドの数学者ウイリアム・ブラウンカーにより示されました。上記のウォリスの公式から導かれたとされます。以下の無限連分数式で表されます。

	double Brouncker(int n){
		int i=0;
		double data=0.0;
		for(i=n;i>0;i--){
			data =( (2*i-1)*(2*i-1) )/(2+data);
		}
		return 4.0/(1.0+data);
	}
  

モンテカルロ法

こちらは式ではなくアルゴリズムの一種になります。

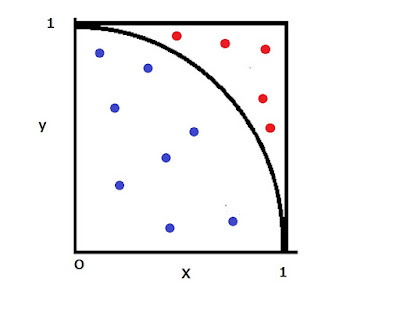
1辺の長さが2の正方形に内接する半径1の円を考えます。この中にランダムに点を打ち込んでいくと、円の範囲に入る点の数とすべての点の数の比が円周率に近づくというものです。下の図でいえば、円周率=(青い点の総数)/(すべての点の総数)と近似できることになります。

今回のプログラムでは円を4等分した領域を考え、4倍することで計算しています。

Ramanujanの公式

インドの数学者シュリニヴァーサ・ラマヌジャンが発見した公式です。収束がとても速いことで知られています。今回のプログラムではn=3で計算しています。これ以上はオーバーフローエラーを起こすため、改変する場合は注意してください。

Gauss=Legendreのアルゴリズム

カール・フリードリヒ・ガウスとアドリアン=マリ・ルジャンドルがそれぞれ研究した反復数値計算アルゴリズムです。

まず初期値を以下のように与えます。

この初期値を次の更新式により計算し、所望の精度(桁数)になるまで繰り返します。

以上の値を用いて、円周率は次の式で近似されます。

ソースコードはこちらに置いておきますので、ご自由にお使いください。

参考

円周率の近似:Wikipedia

円周率:Wikipedia

円周率1,000,000桁表　暗黒通信団